|

배 조종하기라고 해서 거창한 배가 아니라 사각형 2개 삼각형 1개만 움직일 것이다.
텍스쳐도 없는 썰렁한 폴리곤들이다.
다음장에서 ID3DXMatrixStack에 대해서 다루기 위해서 이장을 만들었다.
이 장에서 1. 카메라의 정확한 가로 세로 비율 조정, 2. 배 움직이기 3. 배 렌드링의 순서대로 설명할것이다.
1. 카메라의 정확한 가로 세로 비율 조정
원래 하던 방식대로
D3DXMatrixPerspectiveFovLH( &matProj, D3DX_PI/4, 800.0f/640.0f, 1.0f, 100.0f )
Aspect값에 800.0f/640.0f이란 값을 넣고 정사각형의 폴리곤을 출력했지만, 세로 부분이 길이가 더 짧게 나왔다.
윈도우 모드일때는 타일틀 창 때문에 세로 길이가 실제 길이보다 더 짧아 진다. 정확한 값을 넣기 위해서는
다음과 같이 실제 렌드링되는 윈도우의 클라이언트 크기를 구해서 Aspect에 넣어야 한다.
// Setup Projection
RECT rect;
GetClientRect(hWnd, &rect);
float width = (float)rect.right, height = (float)rect.bottom;
D3DXMatrixPerspectiveFovLH( &matProj, D3DX_PI/4, width/height, 1.0f, 100.0f );
이렇게 하면 가로 세로 길이가 일치하는 정사각형이 나올것이다.
================================================================================================
2. 배 움직이기
배를 움직일때는 현재 좌표에서 움직인 거리를 삼각함수를 이용해 x축으로 얼마 y축으로 얼마 움직였는지 알수있다.
배의 위치를 나타내는 필요한 변수는 다음과 같다.
float g_fx = 0.0f; //현재 x축에서의 위치
float g_fy = 0.0f; //현재 y축에서의 위치
float g_fDegree = 0.0f; //배 본체의 월드에서 향하는 방향
float g_fTurretDegree = 0.0f; //포신의 로컬에서 향하는 방향
void MovPosition(float fMove)
{
#if 1 //y축을 기준으로 회전각을 0으로 할때
double sin_a = -sin( D3DXToRadian(g_fDegree) );
double cos_a = cos( D3DXToRadian(g_fDegree) );
g_fx = float(fMove * sin_a + g_fx);
g_fy = float(fMove * cos_a + g_fy);
#else
double sin_a = sin( D3DXToRadian(g_fDegree) );
double cos_a = cos( D3DXToRadian(g_fDegree) );
g_fy = float(fMove * sin_a + g_fy);
g_fx = float(fMove * cos_a + g_fx);
#endif
}
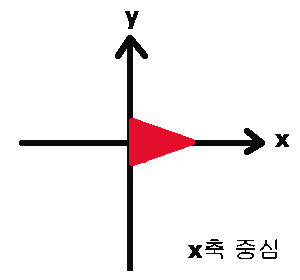
일반적으로 학교에서 배운 수학에서 사용하는 좌표는 X축을 영점 기준으로 잡지만 게임에서는 Y축이나 Z축을
영점 기준으로 잡는다.
X축이 영점일때---
(m은 움직인 거리이다.)
x값은?
cos a = move_x / m
move_x = m * cos a 이므로
목적지 g_fx = move_x + 시작 위치 x = float(fMove * cos_a + g_fx)
y값은?
sin a = move_y / m
move_y = m * sin a 이므로
목적지 g_fy = move_y + 시작 위치 y = g_fy = float(fMove * sin_a + g_fy)
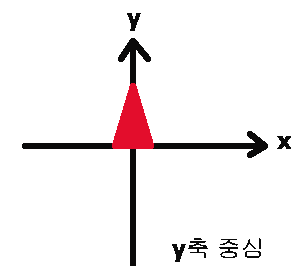
Y축이 영점일 때---
X축과 Y축의 공식이 약간 다를 것이다. 어째서 이렇게 나오지 머리를 싸매고 며칠을 생각한적이 있다.
정석에 나와 있는 삼각함수의 덧셈정리를 한번 쭉~~~ 보자.
|
삼각 함수의 덧셈
정리
1) sin(a
+ b) = sin a * cos b + cos a * sin b
sin(a
- b) = sin a * cos b - cos a * sin b
2) cos(a
+ b) = cos a * cos b - sin a * sin b
cos(a
- b) = cos a * cos b + sin a * sin b
|
x값은?
2번 공식을 적용해보자. y축이 기준이기 때문에 (+90)을 더하면 된다.
cos(a + 90)
= cos a * cos 90 - sin a * sin 90
= cos a * 0 - sin a * 1
그러므로 각도를 구하는 공식은 -sin a이다
-sin a = move_x / m,
move_x = m * (-sin a) 이다.
목적지 g_fx = move_x + 시작 위치 x = float(fMove * sin_a + g_fx)
y값은?
sin(a + 90)
= sin a * cos 90 + cos a * sin 90
= sin a * 0 + cos a * sin 90
그러므로 각도를 구하는 공식은 cos a이다.
cos a = move_y / m
move_y = m * cos a
목적지 g_fy = move_y + 시작 위치 y = g_fy = float(fMove * cos_a + g_fy)
그림을 보면서 삼각함수를 생각하면 이해가 쉬울 것이다.
================================================================================================
3. 배 렌드링
void MoveShip(float fx, float fy)
{
D3DXMATRIX mScale1, mRot1, mTran1, mResult1;
D3DXMATRIX mScale2, mRot2, mTran2, mResult2;
D3DXMATRIX mScale3, mRot3, mTran3, mResult3;
//본체
//SRT
D3DXMatrixScaling( &mScale1, 1.1f, 1.1f, 1.1f );
D3DXMatrixRotationZ(&mRot1, D3DXToRadian(g_fDegree));
D3DXMatrixTranslation( &mTran1, fx, fy, 0.0f);
mResult1 = mScale1 * mRot1 * mTran1;
g_d3d_Device->SetTransform( D3DTS_WORLD, &mResult1);
g_d3d_Device->DrawPrimitive( D3DPT_TRIANGLESTRIP, 3, 2 );
//포탑
D3DXMatrixScaling( &mScale2, 1.0f, 1.0f, 1.0f );
D3DXMatrixRotationZ(&mRot2, D3DXToRadian(g_fTurretDegree));
D3DXMatrixTranslation( &mTran2, 0.0f, -0.7f, 0.0f );
mResult2 = mScale2 * mRot2 * mTran2 * mResult1;
g_d3d_Device->SetTransform( D3DTS_WORLD, &mResult2 );
g_d3d_Device->DrawPrimitive( D3DPT_TRIANGLELIST, 0, 1 );
//포
D3DXMatrixScaling( &mScale3, 0.1f, 0.3f, 1.0f );
D3DXMatrixRotationZ(&mRot3, 0.0f);
D3DXMatrixTranslation( &mTran3, 0.0f, -0.1f, -0.5f);
mResult3 = mScale3 * mRot3 * mTran3 * mResult2;
g_d3d_Device->SetTransform( D3DTS_WORLD, &mResult3 );
g_d3d_Device->DrawPrimitive( D3DPT_TRIANGLESTRIP, 3, 2 );
}
(( 본체 -- 포탑 -- 포 )) 와 같이 모델이 부모에 종속되어 있다.
부모, 자식간의 이동식은 9장에서 본바와 같이 [Lx Ly Lz][Tm child][Tm parent] 순서로
다이렉트 X에서는 행렬을 곱한다. 이동, 회전, 확대는 [Lx Ly Lz][확대][회전][이동]의 순서로
행렬을 곱한다. 이 두가지를 알면 렌더러 소스를 이해하는데 무리가 없을 것이다.
<원 자취(궤적)에 있는 점의 위치 구하기>
구하고자 하는 원 자취의 점을 x1, y1
원점을 x0, y0
반지름을 radius
각도를 angle
x1 = x0 + (cos(angle) * radius);
y1 = y0 + (sin(angle) * radius);
|


