직선의 벡터 방정식
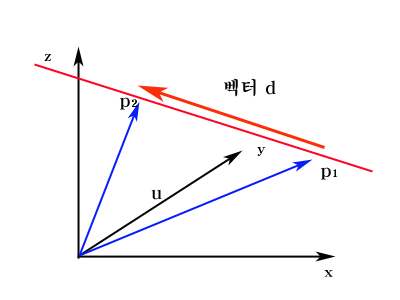
1. 점 P1를 통과하고 벡터 d의 방향을 가지고 있을 때 직선을 벡터 형식으로 표현하면 다음과 같다.
p = P1 + ud
[1, 2번에 관련된 참조 그림]
2. 두 개의 점 P1와 P2를 통과하는 직선을 벡터 형식으로 표현하면 다음과 같다.
p = P1 + u (P2 - P1 )
한점과 직선의 최단거리 구하기
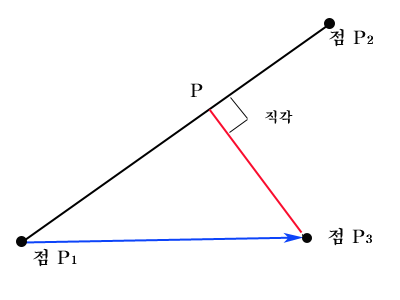
점 P1 , P2를 지나는 벡터의 직선과 점 P3의 최단거리를 구해보자.
이때, 직선위의 최단거리 점의 위치를 점 P라고 하자.
직선 벡터 (P2 - P1 )는 d라고 한다.
1. 직선의 방정식에 의해 최단거리 점 P는
P = P1 + u (P2 - P1 ) = P1 + ud
2. 벡터의 직선과 점 P3에서 내려 오는 직선은 직각이므로
( P3 - P ) dot ( P2 - P1 ) = 0
3. 2번의 P에 P = P1 + ud를 대입한다.
( P3 - P1 - ud ) dot d = 0
(P3 - P1) dot d - ud dot d = 0
( ( P3 - P1 ) dot d ) = u (d dot d)
u = ( ( P3 - P1 ) dot d ) / (d dot d)
두벡터 a와 b가 같은 경우(a = b) 내적은 다음과 같다.
| a dot b = || a ||² |
그러므로 결과는 아래와 같다.
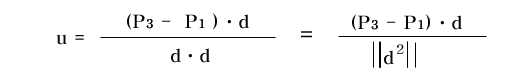
[펌] 한빛 미디어 : 좋은 게임을 만든는 핵심 원리 147페이지