벡터의 직선 방정식에 대해서 알아 보자.

<< 2차원 직선의 방정식 >>

1. 기울기와 한점을 알때 기울기가  m과 한 점(x1, y1)을 지나는 직선은 y = m ( x - x1 ) + y 이다.

예) 기울기가 2이고 점( 1, 3 )을 지나는 직선 : y = 2( x - 1 ) + 3 = 2x + 1

2. 두점을 알때

두점  ( x1, y1 ), ( x2, y2 )를 지나는 직선은 y =  ( y2 - y1 ) / ( x2 - x1 ) * ( x - x1 ) + y1 이다.
두점 ( 1, 2 ), ( 3, 6 )을 지나는 직선은 y = ( 6 - 2 ) / ( 3 - 1 )  *  ( x - 1 ) + 2 = 2x

<< 3차원 직선의 방정식 >>

1. 한 점을 지나고 벡터와 평행 할 때 ( 벡터는 직선의 방향 벡터로 기울기의 역할이다 ) 한 점을 ( x1, y1, z1 )을 지나고 벡터 u = ( a, b, c )와 평행한 직선은 ( x - x1 ) / a = ( y - y1 ) / b = ( z - z1 ) / c 로 표현한다.

예) 점 ( 1, 2, 3 )을 지나고 벡터 v = ( 2, 1, 3 )에 평행한 직선은 ( x - 1 ) / 2 = y - 2 = ( z - 3 ) / 3이다.

2. 두점 ( x1, y1, z1 ), ( x2, y2, z2 )를 지나는 직선은

( x - x1 ) / ( x2 - x1 ) / ( x2 - x1 ) = ( y - y1 ) / ( y2- y1 ) = ( z - z1 ) / ( z2 - z1 )

예) 두 점 ( 1, 2, 3 ), ( 2, 4, 6 )을 지나는 직선은 x - 1 = ( y - 2 ) / 2 = ( z - 3 ) / 3이다.

직선 ( x - x1 ) / a = ( y - y1 ) / b = ( z - z1 ) / c 은 ( x - x1 ) / a과 ( y - y1 ) / b 의 교선이며, 이 직선 위의 점의 좌표는 매개변수 t를 써면 다음과 같다.

3. 공간상의 두 직선의 각도를 알고 싶을 때

두 직선의 방향 벡터를 u1 = ( a1, b1, c1 ), u2 = ( a2, b2, c2 )라고 할 때 예각의 크기는
cos θ = | u1 ㆍ u2 |  /  | u1 | | u2 |  

<< 3차원 직선의 방정식 3가지 표현 >>

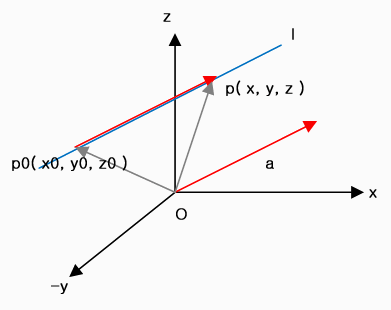
한 점 p0 ( x0, y0, z0 )를 지나고 영아닌 벡터 a = ai + bj + ck에 평행한 직선은 벡터 a와

한 점 p0 ( x0, y0, z0 )를 지나고 영아닌 벡터 a = ai + bj + ck에 평행한 직선은 벡터a

가

평행 즉 아래와 같은 식이 성립된다.

식 1로부터

                  ( x - x0 )i + ( y - y0 )j + ( z - z0 )k = tai + tbj + tck

그러므로 직선의 방정식은 다음과 같이 세가지로 나타낼 수 있다.

i) 매개변수 방정식 (parametric equations)

             x = x0 + ta
             y = y0 + tb    ( -∞ < t < +∞ )
             z = z0 + tc

ii) 벡터방정식 (vector equations)

p = p0 + ta,

iii) 대칭 방정식

( x - x0 ) / a = ( y - y0 ) / b = ( z - z0 ) / c,   ( a, b, c는 0이 아니다. )

예제) 점 P(2, -1, 3)를 지나고 벡터 a = -3i + 2j + 4k에 평행한 직선의 방정식은 다음 세가지로 나타낼수 있다.

i) x = 2 - 3t
  y = -1 + 2t    ( -∞ < t < +∞ ) -
  z = 3 + 4t

ii) xi + yj + zk = 2i - j + 3k + ( -3i + 2j + 4k )t

iii) ( x - 2 ) / -3 = ( y + 1 ) / 2 = ( z - 3 ) / 4

참고)

http://masil.info/tag

http://user.chol.com/~SDHBKH/6th/math2/source3/vector(04).ppt

http://matrix.skku.ac.kr/sglee/krf-1/linearalgebra/multimediaproject/5week/20501/page1.htm