축 방향에 의한 자르기를 해보자. 축으로 자르고 나면 삼각형 메쉬로 보여줄려면 삼각화 작업과 노멀 값을 구하는 작업도 필요하다.
폴리곤 자르기
< X축 , Y축, Z축의 한 축의 값을 알때 다른 축의 값 구하기 >
폴리곤은 라인으로 구성 되어 있고, 라인은 선형이므로, 한 시작점과 끝점을 알고 있다면 선형 보간이나 직선의 방정식을 이용해 다른 축의 좌표를 구 할 수 있다.
그림 1 처럼 X 축의 좌표가 10, 0, 10일때, 5에서 자르는 경우를 생각해 보자.
그림 1) x 축의 좌표

직선의 방정식에 의해 자르면 다음식을 이용한다.
|
= |
|
= |
|
직선의 방정식을 이용한 함수는 다음과 같다.
|
inline float LinearEquation( float x, float x1, float x2, float y1, float y2 ) { float y = ( x - x1 ) * ( y2 - y1 ) / ( x2 - x1 ) + y1; return y; } |
보간을 이용한 방식은 다음과 같다.
그림 2)보간을 이용하는 경우

보간을 이용하는 경우 자르는 지점을 0으로 만든다. 그림 1을 보간으로 이용하기 위해 변환하면 그림2와 같다.
변환 된 값은 -5, 0, 5이다 . a에서 c에 대한 b의 보간을 구하면 다음과 같다.
보간의 값 s = a/( a - c ) 나 s = ( -a )/( c - a ) 로 나타낼수 있다.
< 연속된 라인의 자르기 >
라인을 자르는 경우의 수는 다음과 같다. 그림2와 같이 절단점을 0으로 변환후 음수와 양수로 고려해서 생각한다.
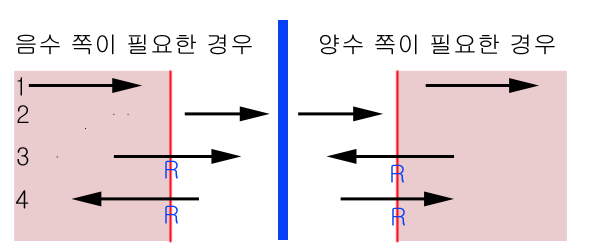
시작점을 a, 끝점을 b, 중간에 절단되는 점을 R이라 하자.
(1) 두점이 모두 포함되는 경우 : b점 추가
(2) 두점이 모두 포함되지 않는 경우 : 추가 점 없음
(3) 시작점점이 포함된 경우: R 추가
(4) 끝점이 포함된 경우: R 추가, b점 추가
(3), (4)와 같이 시작점과 끝점의 부호가 다르면 절단이 일어나는 경우이다.
끝점이 저장 되는 경우는 음수쪽일때는 음수, 양수쪽일때는 양수이면 저장한다.
직선의 방정식에 의한 함수: ClipPolyLine1(....), ClipPolySimple(....)
보간에 의한 함수: ClipTriangle(....)
매개 변수는 3개의 함수 모두 똑같으니 ClipPolyLine1만 살펴 본다.
ClipPolyLine1의 리턴값은 직선의 방정식에 의해 점의 갯수를 리턴한다.
D3DXVECTOR3* in : 입력되는 폴리곤의 점이다.
int n : 점의 갯수이다.
float out : x, y, z 3차원 점을 float 포인터에 의해 반환한다.
float nx, ny, nz : 자르고자 하는 축을 3개 중에 하나만 -1이나 1로 설정하고 나머지 2개의 값은 0으로 한다.
-1이면 pd값보다 작은 값을 남기고 큰값을 잘라낸다.
1이면 pd값보다 큰값을 남기고 작은 값을 잘라낸다.
float pd : 자를때 기준이 되는 축의 값이다.
변수 i는 목표점이고, j는 시작점이다.
|
int ClipPolyLine1( const D3DXVECTOR3* in, int n, float* out, float nx, float ny, float nz, float pd ) { float d[12];
float basis = (nx + ny + nz) * pd; for (int i = 0; i < n; ++i) d[i] = nx*in[i].x + ny*in[i].y + nz*in[i].z - basis;
int m = 0; float x = pd; //라인에 대해서 검사 for (int i = 0, j = n-1; i < n; j=i, ++i) { bool ina = d[j] >= 0; bool inb = d[i] >= 0; if (ina != inb) { if( nx != 0 ) { out[m*3+0] = pd; out[m*3+1] = LinearEquation( pd, in[j].x, in[i].x, in[j].y, in[i].y ); out[m*3+2] = LinearEquation( pd, in[j].x, in[i].x, in[j].z, in[i].z ); } else if( ny != 0 ) { out[m*3+1] = pd; out[m*3+0] = LinearEquation( pd, in[j].y, in[i].y, in[j].x, in[i].x ); out[m*3+2] = LinearEquation( pd, in[j].y, in[i].y, in[j].z, in[i].z ); } else { out[m*3+2] = pd; out[m*3+0] = LinearEquation( pd, in[j].z, in[i].z, in[j].x, in[i].x ); out[m*3+1] = LinearEquation( pd, in[j].z, in[i].z, in[j].y, in[i].y ); } m++; } if (inb) { out[m*3+0] = in[i].x; out[m*3+1] = in[i].y; out[m*3+2] = in[i].z; m++; } }
return m; } |
보간을 이용한 함수는 다음과 같다.
|
int ClipPolyLine(const D3DXVECTOR3* in, int n, float* out, float nx, float ny, float nz, float pd) { float d[12];
if( nx + ny + nz > 0 ) pd = -pd; for (int i = 0; i < n; ++i) d[i] = nx*in[i].x + ny*in[i].y + nz*in[i].z + pd;
int m = 0; //라인에 대해서 검사 for (int i = 0, j = n-1; i < n; j=i, ++i) { bool ina = d[j] >= 0; bool inb = d[i] >= 0; if (ina != inb) { float s = d[j] / (d[j] - d[i]); //길이에 대한 보간으로 전체 길이에 대한 d[j]의 비율
out[m*3+0] = in[j].x + (in[i].x - in[j].x)*s; // b + ( b - a ) * s 는 pd를 기준으로 하는 좌표이다. out[m*3+1] = in[j].y + (in[i].y - in[j].y)*s; out[m*3+2] = in[j].z + (in[i].z - in[j].z)*s; m++; } if (inb) { out[m*3+0] = in[i].x; out[m*3+1] = in[i].y; out[m*3+2] = in[i].z; m++; } } return m; } |
삼각화 (Triangulation)
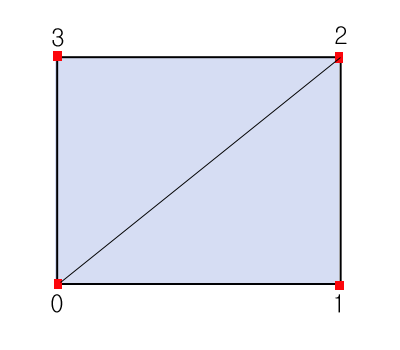
폴리곤을 한 축에 의해서 자르면 점이 3개에서 4개로 된다. 다이렉트 X에서 폴리곤을 표시 할려면 삼각형으로 변환 되어야 한다. 한 축이 잘리고 나서 사각형이기 때문에, 복잡한 삼각화 알고리즘을 사용 할 필요가 없다. 오른손 좌표이기 때문에 시계 반대 방향으로 2개의 삼각형을 저장하면 된다.
첫 번째 삼각형 0, 1, 2
둘째 삼각형 0, 2, 3
DxPolygon::ClipAxis에서 else if( n == 4 )인 경우 하나의 삼각형을 더 저장한다.
노멀 값 구하기
ComputePolygonNormal(....)에 의해서 노멀값을 구한다.
자신의 트라이앵글만 구하는 간단한 방법과 자신과 인접하고 있는 모든 폴리곤을 더해서 노멀값을 구하여 부드러운 폴리곤을 구하는 방식이 있다. 주위의 폴리곤을 더하여 노멀값을 구하면 계산 시간이 많이 걸린다.
여기서는 인덱스를 사용하지 않았기 때문에 같은 좌표인지 체크 하는라 시간이 많이 걸렸다.

ComputeNormal() 노멀값을 구할 때 불리는 기본 함수이다.
|
void ComputeNormal( D3DXVECTOR3* out, D3DXVECTOR3* p0, D3DXVECTOR3* p1, D3DXVECTOR3* p2 ) { D3DXVECTOR3 u = *p1 - *p0; D3DXVECTOR3 v = *p2 - *p0;
D3DXVec3Cross(out, &u, &v); D3DXVec3Normalize(out, out);
/* D3DXVECTOR3 out; D3DXVECTOR3 p0 = D3DXVECTOR3( -1, -1, 0 ); D3DXVECTOR3 p1 = D3DXVECTOR3( -1, 1, 0 ); D3DXVECTOR3 p2 = D3DXVECTOR3( 1, 0, 0 );
ComputeNormal( &out, &p0, &p1, &p2 ); //0, 0, -1 --> 왼손 좌표계에서는 시계방향으로 구한다. ComputeNormal( &out, &p0, &p2, &p1 ); //0, 0, 1 --> 오른손 좌표계에서는 반시계방향으로 구한다. */ } |
ComputePolygonNormal()은 실제로 노멀값을 구하여 버텍스 버퍼에 노멀값을 입력하고 있다.
간단하게 구할 때는 ComputeNormal()을 이용하여 노멀값을 추가하면 끝이다.
|
void ComputePolygonNormal( DxPolygon* polygon ) { PointArray& vrtArr = polygon->GetPosition(); int nSize = (int)vrtArr.size(); assert( nSize >= 3 );
D3DXVECTOR3 out; for( int i = 0; i < nSize; i += 3 ) { D3DXVECTOR3 v0( vrtArr[i].x, vrtArr[i].y, vrtArr[i].z ); D3DXVECTOR3 v1( vrtArr[i+1].x, vrtArr[i+1].y, vrtArr[i+1].z ); D3DXVECTOR3 v2( vrtArr[i+2].x, vrtArr[i+2].y, vrtArr[i+2].z ); ComputeNormal( &out, &v0, &v1, &v2 ); polygon->PushBackNormal( DataType::Point3( out.x, out.y, out.z ) ); polygon->PushBackNormal( DataType::Point3( out.x, out.y, out.z ) ); polygon->PushBackNormal( DataType::Point3( out.x, out.y, out.z ) ); } } |
<부드러운 폴리곤의 노멀값을 구하기>
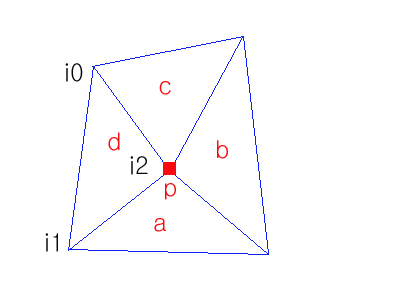
인덱스 버퍼를 사용하지 않는 버텍스의 버퍼의 경우 그림처럼 12(4개의 삼각형)개의 버텍스가 사용된다.
한점당 공유되는 모든 삼각형의 노멀값을 더해서 다시 정규화 하면 폴리곤이 부드럽게 보인다.
1. 공유 버텍스 인덱스 구하기
for 버텍스 갯수 만큼 반복
{
if( 버텍스 위치가 같으면 )
버텍스 인덱스 저장( 자신은 저장 하지 않는다 )
}
2. 노멀값 더하기
for 버텍스 갯수 만큼 반복 step 폴리곤이으로 3만큼 증가
{
3개의 버텍스 노멀값 계산
공유 버텍스의 인덱스를 이용하여 i0와 공유하는 버텍스의 노멀값에 현재 노멀값을 모두 더한다.
공유 버텍스의 인덱스를 이용하여 i1와 공유하는 버텍스의 노멀값에 현재 노멀값을 모두 더한다.
공유 버텍스의 인덱스를 이용하여 i2와 공유하는 버텍스의 노멀값에 현재 노멀값을 모두 더한다.
}
3. 노멀값 정규화 하기
for 버텍스 갯수 만큼 반복
{
노멀 정규화
}
|
void ComputePolygonNormal( DxPolygon* polygon ) { typedef std::vector<int> IndexArrayComponent;
PointArray& vrtArr = polygon->GetPosition(); int nSize = (int)vrtArr.size(); if( nSize < 3 ) return;
//assert( nSize >= 3 ); D3DXVECTOR3* normal = new D3DXVECTOR3[ nSize ]; memset( normal, 0, nSize * sizeof( D3DXVECTOR3 ) );
IndexArrayComponent* sharedNormalIndex = new IndexArrayComponent[ nSize ]; for( int i = 0; i < nSize; ++i ) { for( int k = 0; k < nSize; ++k ) { if( i != k ) { if( vrtArr[i].x == vrtArr[k].x && vrtArr[i].y == vrtArr[k].y && vrtArr[i].z == vrtArr[k].z ) { sharedNormalIndex[i].push_back( k ); } } } }
D3DXVECTOR3 out; for( int i = 0; i < nSize; i += 3 ) { D3DXVECTOR3 v0( vrtArr[i].x, vrtArr[i].y, vrtArr[i].z ); D3DXVECTOR3 v1( vrtArr[i+1].x, vrtArr[i+1].y, vrtArr[i+1].z ); D3DXVECTOR3 v2( vrtArr[i+2].x, vrtArr[i+2].y, vrtArr[i+2].z ); ComputeNormal( &out, &v0, &v1, &v2 );
normal[i+0] += out; normal[i+1] += out; normal[i+2] += out;
int nCount = (int)sharedNormalIndex[i].size(); IndexArrayComponent& indexArr0 = sharedNormalIndex[i]; for( int k = 0; k < nCount; ++k ) { int index = indexArr0[k]; normal[ index ] += out; }
nCount = (int)sharedNormalIndex[i+1].size(); IndexArrayComponent& indexArr1 = sharedNormalIndex[i+1]; for( int k = 0; k < nCount; ++k ) { int index = indexArr1[k]; normal[ index ] += out; }
nCount = (int)sharedNormalIndex[i+2].size(); IndexArrayComponent& indexArr2 = sharedNormalIndex[i+2]; for( int k = 0; k < nCount; ++k ) { int index = indexArr2[k]; normal[ index ] += out; } }
for( int i = 0; i < nSize; ++i ) { D3DXVec3Normalize(&normal[i], &normal[i]); polygon->PushBackNormal( DataType::Point3( normal[i].x, normal[i].y, normal[i].z ) ); }
delete [] normal; delete [] sharedNormalIndex; } |
최종 결과는 다음과 같다.
비너스 상을 x축으로 자른 화면이다.

위에서 nx가 -1이므로 x축으로 잘리고 음수 값이므로 양수축의 값이 잘려 나간다.
basis가 0이므로 x축의 0의 값을 기준으로 자른다.