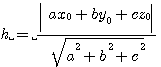<직선의 방정식>

점A(x1, y1, z1)을 지나고 벡터 u =(a, b, c)에 평행한 직선의 방적식은

<평면의 방정식>

1. 점 (x1, y1, z1)을 지나고, 벡터 v = ( a, b, c )에 수직인 평면의 방정식은

a(x - x1) + b(y - y1) + c(z - z1) = 0

-> ax + by + cz - (ax1 + by1 + cz1) = 0

-> ax + by + cz + d = 0

여기서 a, b, c는 노멀 벡터의 세 성분, d는 평면과 원점까지의 최단거리이다.

2. 세 점 A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3)를 지나는 평면의 방정식

ax + by + cz + d = 0

a = y1(z2 - z3) + y2(z3 - z1) + y3(z1 - z2)
b = z1(x2 - x3) + z2(x3 - x1) + z3(x1 - x2)
c = x2(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)

d = -(x1(y2x3 - y3z2) + x2(y3x1 - y1z3) + x3(y1x2 - y2z1))

<점과 평면 사이의 거리>

점 (x0, y0, z0)에서 평면 ax + by + cz + d = 0까지 거리 h는