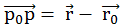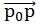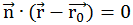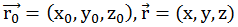세점을 알고 있을때 평면의 법선 벡터 구하기
Calculate the vector normal to the plane by given points평면상의 점 A, B, C가 있을때 법석 벡터를 구할려면
B-A 벡터와 C-A 두개의 벡터를 외적하면 된다.
|
|
|
|
소스로 표현하면 다음과 같다.
Dir = (B - A) x (C - A)
Norm = Dir / len(Dir)
========>
class Plane {
Vector3 a, b, c;
public Vector3 Normal {
get {
var dir = Vector3.Cross(b - a, c - a);
var norm = Vector3.Normalize(dir);
return norm;
}
}
}
Norm = Dir / len(Dir)
========>
class Plane {
Vector3 a, b, c;
public Vector3 Normal {
get {
var dir = Vector3.Cross(b - a, c - a);
var norm = Vector3.Normalize(dir);
return norm;
}
}
}
더 자세한 설명을 원하면 다음링크를 참조한다.
세점의 방향 판단(tutorial09.html)
평면의 벡터 방정식
|
|||
|

|
||||||||
|
또한
|
|||
|
|||
|

평면의 방정식
|
|||
| (a, b, c)ο(x-x0, y-y0, z-z0) = 0이다. |
|||
| 즉, a(x-x0) + b(y-y0) + c(z-z0)=이다. | |||
| 간단하게 d = -ax0 - by0 -cz0라 하면 평면의 방정식은 ax+by+cz+d=0이다. |
참고)
평면의 방정식 내용은 Nenyafle님의 블로그 내용을 많이 가져 왔습니다.
http://m.blog.naver.com/mindo1103/90103407031
http://200315193.tistory.com/503
http://dolphin.ivyro.net/file/mathematics/tutorial15.html